Kakuro-Strategien
Die Anzahl der Kakuro-Strategien ist nicht ganz so enorm wie die der Sudoku-Strategien. Dennoch gibt es hier einige interessante Methoden. Auf dieser Seite will ich auf einige davon eingehen.
Eine der grundlegendsten Strategien habe ich bereits auf der Seite zu den Kakuro-Regeln kurz beschrieben. Auch hier beschäftigen wir uns zuerst damit. Für noch mehr Informationen und viele Beispiele können Sie sich auch gerne mein Buch zu Kakuro-Löungsstrategien anschauen.
Eindeutige Summen
Manche Summen in Kakuro sind eindeutig. Das heißt, es gibt nur eine Kombination an Summanden, die eingetragen werden kann. Das einfachste Beispiel ist die 3. Diese lässt sich nur aus 1 und 2 bilden (0+3 ist nicht erlaubt, da nur Zahlen von 1 bis 9 verwendet werden dürfen). Die höchste eindeutige Summe (und die höchste überhaupt) ist die 45. Sie ist die Summe aus allen Zahlen von 1 bis 9.
Wer sich etwas tiefergehend mit Mathematik beschäftigt hat, dem werden diese Summen vielleicht bekannt vorgekommen sein. Sie lassen sich aus der Gaußschen Summenformel errechnen. Diese geht auf Carl Friedrich Gauß zurück, einen der bedeutendsten Mathematiker der Geschichte (Er war früher auf dem Zehn-Mark-Schein abgebildet).
Bei der Gaußschen Summenformel kann auf einfache Art und Weise die Summe der ersten aufeinanderfolgenden natürlichen Zahlen gebildet werden. Sie lautet
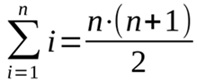
Für die Summe der ersten 9 Zahlen gilt also, wenn man die 9 für n einsetzt, 1+2+3+4+5+6+7+8+9 = (9x10)/2 = 45.
Aber keine Angst, Sie müssen außer den Grundrechenarten und etwas Logik keine großartige Mathematik beherrschen, um ein Kakuro zu lösen. Dies war nur ein kurzer Ausflug.
Liste mit eindeutigen Summen
Um die Sache zu erleichtern, habe ich eine Liste mit allen möglichen Kombinationen für alle Summen in Kakuro zusammengestellt (PDF). Die eindeutigen Summen habe ich jeweils grau markiert. Insgesamt gibt es in Kakuro 502 mögliche Kombinationen.
Die Vorgehensweise ist nun wie folgt:
- Schritt 1: Suche nach einer eindeutigen Summe
- Schritt 2: Schreibe diese Summanden an den Rand, mit Bleistift in die Felder oder behalte sie im Kopf.
- Schritt 3: Schaue nach den Schnittpunkten zwischen solchen Summen, ob es dort nur eine gemeinsame mögliche Ziffer gibt.
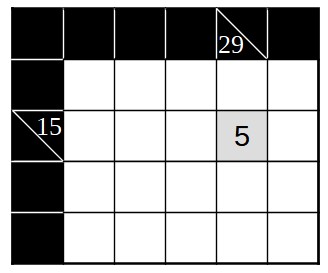
Nehmen wir als Beispiel die Summe 15 mit 5 Summanden und die 29 mit 4 Summanden. Beide Summen sind eindeutig. Die 15 lässt sich nur aus 1, 2, 3, 4 und 5 bilden, die 29 nur aus 5, 7, 8 und 9. Wenn diese beiden Summen sich auf dem Spielfeld kreuzen (siehe nachfolgendes Bild), muss im Schnittpunkt eine Zahl stehen, die in beiden Varianten vorkommt. Das ist hier nur die 5, weshalb wir diese im Schnittpunkt eintragen können.
Nicht-eindeutige Summen mit nur einer Möglichkeit
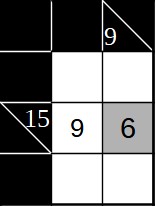
Die oben beschriebene Kakuro-Strategie lässt sich auch anwenden, wenn eine der beiden Summen nicht eindeutig ist, falls es trotzdem nur eine Möglichkeit gibt, die Summen zu kombinieren. Dabei muss man nur etwas Logik einsetzen. Schauen wir uns hierfür die folgende Situation an:

Hier müssen die 15 mit zwei Summanden und die 9 mit drei Summanden gebildet werden. Keine der beiden Summen ist eindeutig. Für die 15 gibt es zwei Möglichkeiten: 7+8 oder 6+9. Für die 9 gibt es drei Möglichkeiten: 1+2+6, 1+3+5 oder 2+3+4. Im Schnittpunkt dieser beiden Summen muss nun aber eine Zahl stehen, die in beiden Varianten vorkommt. Dafür gibt es hier nur eine Möglichkeit: die 6. Sie kommt sowohl in 6 + 9 = 15 als auch in 1 + 2 + 6 = 9 vor. Also können wir die 6 dort eintragen.
Auch hierfür ist die oben verlinkte Tabelle mit den verschiedenen Kombinationen sehr hilfreich. Nehmen wir als weiteres Beispiel die Summe 32, die mit fünf Summanden gebildet werden soll. Hierfür gibt es drei Möglichkeiten (siehe PDF-Datei). Allerdings enthält keine dieser Möglichkeiten eine 1. Grenzt also eine andere Summe an, in der die 1 vorkommen muss (beispielsweise 7 = 1 + 2 + 4), können wir für den Schnittpunkt dieser beiden Summen die 1 ausschließen.
Ich würde allerdings dazu raten, diese Tabelle nur zu Rate zu ziehen, wenn man nicht mehr weiter kommt, und es vorher mit eigenen Überlegungen zu probieren. Das ist ja der eigentliche Sinn eines Zahlenrätsels.
Subtraktionstechnik als Kakuro-Strategie
Wie eine solche Überlegung aussehen kann, sehen wir am nächsten Beispiel. Hierbei handelt es sich um ein 6x6-Kakuro, also eine recht einfache Variante. Die einfachsten Bereiche, wie z.B. die Ecke rechts unten, sind bereits ausgefüllt.
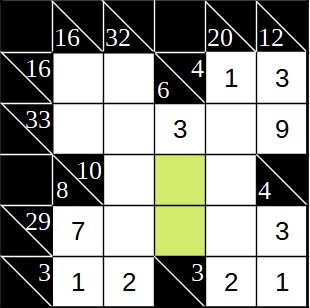
Wir interessieren uns hier für die beiden grün markierten Felder. Für diese kommen nur die 1 und die 2 in Frage, um gemeinsam mit der 3 die Summe 6 zu bilden. Wir wissen aber noch nicht, in welcher Reihenfolge die beiden Zahlen eingetragen werden müssen.
Diese Summe kreuzt sich mit der Summe 29, die aus 5 Summanden besteht. Mit 3 und 7 stehen zwei davon schon fest. Wir können uns nun anschauen, was passieren würde, wenn im unteren grünen Feld die 1 oder die 2 steht. Steht dort die 1, haben wie die Zwischensumme 1 + 3 + 7 = 11. Für die beiden noch übrigen Felder können wir also die 11 von der Gesamtsumme abziehen.
29 minus 11 ergibt 18. Die beiden restlichen Felder müssen also zusammen 18 ergeben. Das ist aber nach den Kakuro-Regeln nicht möglich. Die Summe 9 + 9 ist nicht erlaubt, da jede Ziffer von 1 bis 9 nur jeweils einmal in einer Summe vorkommen darf. Also können wir hier die 1 ausschließen und die 2 eintragen.
Fallunterscheidung mit Kombinationen von Kandidaten
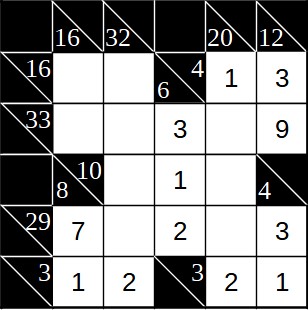
Das obige Beispiel können wir nun noch etwas fortsetzen. Nachdem auch die Ecke links oben ausgefüllt ist, bleibt nur noch das Zentrum des Spielfelds. Für die beiden waagerechten Summen 33 und 29 bleiben nur noch zwei Felder offen. Aufgrund der Regeln und der Subtraktionsmethode wissen wir auch, welche beiden Ziffern jeweils noch fehlen.
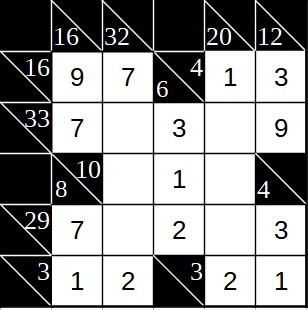
Für die Summe 33 bleibt noch ein Rest von 14 (33 – 3 – 7 – 9). Diese lässt sich nur aus 6 und 8 bilden (denn 7+7 ist ja nicht erlaubt und 5+9 ebenfalls nicht, da die 9 bereits vorhanden ist). Bei der Summe 29 bleibt noch eine Restsumme von 17 (29 – 2 – 3 – 7). Hierfür kommen nur 8 und 9 in Frage. Wir müssen nun nur noch festlegen, in welcher Reihenfolge die Zahlen dort eingetragen werden. Im Bild unten sind die Kandidaten eingetragen (das könnte man z.B. mit Bleistift machen).
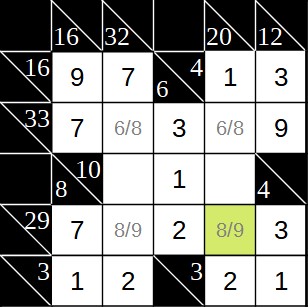
Wir können uns nun anschauen, was geschieht, wenn wir in das grün markierte Feld die 9 eintragen. Dabei achten wir auf die Wechselwirkungen mit der senkrechten Summe 20.
Steht im grünen Feld eine 9, stünde im Feld darüber eine 8 (die 9 führt zur 8 weiter links in der Zeile, die wiederum zur 6 in Zeile 3 und diese wiederum zur 8 in der gleichen Spalte). Damit hätten wir in der Spalte mit Summe 20 1 + 2 + 8 + 9 = 20. Allerdings bleibt ja noch ein Feld frei. Und da dort keine 0 eingetragen werden darf, sind wir auf einen Widerspruch gestoßen. Im grünen Feld darf also nicht die 9 stehen, sondern nur die 8. Anschließend lässt sich der Rest einfach lösen. Die Lösung sieht wie folgt aus:
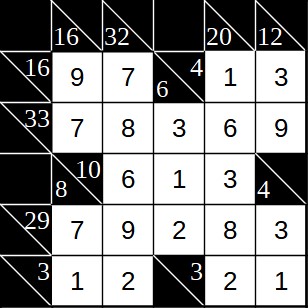
Eine weitere Kakuro-Strategie ist es, Kandidaten als Platzhalter einzutragen.
