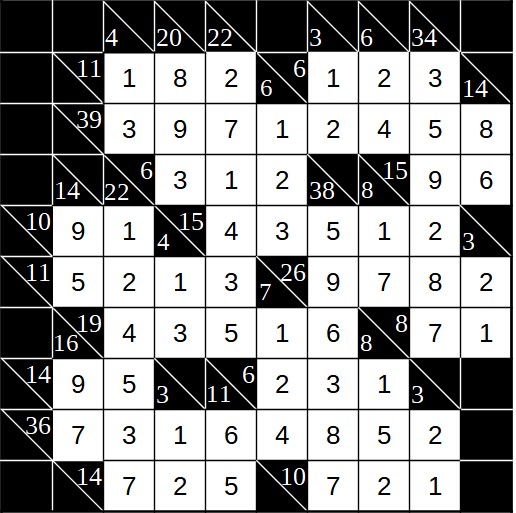
Kakuro Beispiel 2 (10x10)

Das folgende Kakuro-Beispiel gehört in die Kategorie einfach bis leicht fortgeschritten. Es handelt sich um ein 10x10-Kakuro (d.h. zehn Zeilen und zehn Spalten). Natürlich gilt auch hier, dass der vorgeschlagene Lösungsweg nur ein Vorschlag ist. Man könnte auch anders vorgehen.

Zu Beginn haben wir die folgende Situation:

In Zeile 2 haben wir u.a. die Summe 6 mit drei Ziffern. Dies ist eine eindeutige Summe, sie lässt sich nur aus 1, 2 und 3 bilden. Senkrecht schneidet sich diese Summe mit der 3 (1 + 2) und der 6. Die 3 kann in keiner dieser beiden Summen vorkommen, da wir ansonsten 3 + 3 = 6 hätten, was ein Widerspruch zu den Kakuro-Regeln ist. Also muss die 3 in das rechte der drei Felder der Summe 6.

Anschließend können wir die Summe 3 in der letzten Spalte anschauen. Diese kreuzt sich mit der 26 aus vier Summanden. Würden wir oben die 1 einsetzen, hätten wir für die Summe 26 einen Rest von 25. Die maximale Summe aus drei Feldern ist aber 24 (7 + 8 + 9). Daher muss für die Summe 3 oben die 2 und unten die 1 eingetragen werden.

Für die Summe 26 bleiben dann die oben angesprochenen 24 Rest. Wir haben hier eine Kreuzung mit Summe 8 aus zwei Ziffern. Teil dieser Summe kann weder die 9 noch die 8 sein, weshalb hier nur die 7 bleibt. Damit ergibt sich folgendes Bild.

Als nächstes können wir uns die Summe 38 mit sechs Summanden anschauen. Hier handelt es sich ebenfalls um eine eindeutige Summe, da sie nur mit 3, 5, 6, 7, 8 und 9 gebildet werden kann. Im Schnittpunkt mit der Summe 6 (1 + 2 + 3) muss hier die 3 stehen, da weder 1 noch 2 in der 38 vorkommen. Weiter oben schneidet sich die 38 außerdem mit einer weiteren eindeutigen Summe, der 15 (1 + 2 + 3 + 4 + 5). Da die 3 bereits vergeben ist, haben die Summe 38 und die 15 nun nur noch die 5 gemeinsam. Sie muss daher in den Schnittpunkt eingetragen werden.

Links unten gibt es auch einen eindeutigen Schnittpunkt. Es handelt sich um den Schnittpunkt aus der Summe 14 und der 16 (beide mit zwei Summanden). Die 16 ist mit 7 + 9 eindeutig. Würden wir in den Schnittpunkt die 7 schreiben, bliebe für die 14 ein Rest von 7. Zweimal 7 in einer Summe ist aber nicht erlaubt. Daher kommt die 9 in den Schnittpunkt.

Etwas weiter oben gibt es mit der 11 aus vier Ziffern eine weitere eindeutige Summe, die sich aus 1, 2, 3 und 5 bilden lässt. Diese schneidet sich mit der 14. Für die 14 gibt es zwei Möglichkeiten: 6 und 8 oder 5 und 9. Von dieser Ziffern kommt aber nur die 5 auch in der Summe 11 vor, weshalb sie in den Schnittpunkt muss. Für das andere Feld bleibt die 9.

Eine Möglichkeit wäre nun, sich die Situation oben links anzuschauen. Dort schneiden sich die Summen 20 und 6. Die 6 mit drei Summanden haben wir bereits zweimal gesehen. In den Schnittpunkt der beiden Summen muss die 3 eingetragen werden, da mit der 1 und der 2 ein zu großer Rest für die 20 bliebe. Damit bleibt für die 20 ein Rest von 17, also 8 und 9. Wenn wir die 9 in das obere der beiden Felder schreiben, bleibt für die Summe 11, die hier kreuzt, ein Rest von 2 mit zwei Feldern. Dies ist aber nicht möglich. Also kommt die 8 nach oben und die 9 darunter.

Damit sind auch die anderen beiden Felder der Summe 11 klar. Links oben kann die 2 nicht stehen, da wir ansonsten 2 + 2 = 4 hätten, was den Regeln widerspricht. Mit diesen Überlegungen ergibt sich nun folgendes Bild:

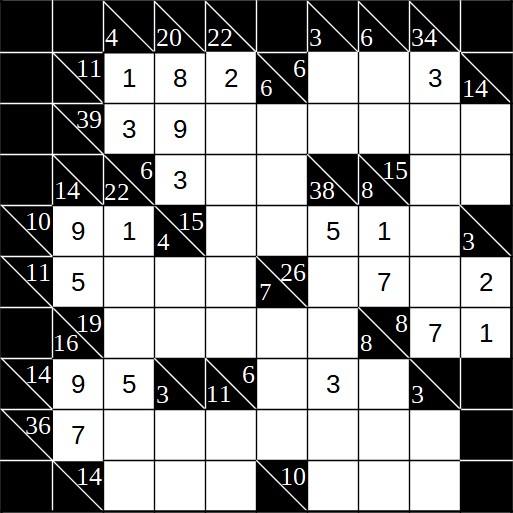
Jetzt lassen sich mehrere kleine Zahlen eintragen. Für die Summe 6 (Zeile 4, Spalte 3) müssen wir noch 1 und 2 eintragen. Seit dem letzten Schritt haben wir aber bereits eine 2 in der Spalte mit Summe 22. Daher ist die Reihenfolge klar. Auch die andere Summe 6 lässt sich lösen, da hier bereits eine 3 in der Zeile mit Summe 39 eingetragen ist. Die Zeile mit Summe 15 lässt sich mit der gleichen Logik lösen.

Damit ist auch die Situation rechts oben klar, da es auch hier nur noch jeweils eine Möglichkeit gibt:

Nun können wir uns erneut auf der linken Seite die Summe 11 mit vier Summanden anschauen. Die 5 ist bereits eingetragen, bleiben also noch 1, 2 und 3 für die drei restlichen Felder. Diese Zeile schneidet sich mit der Summe 22, in der bereits 1 und 2 vorhanden sind. Bleibt also nur die 3 für das Feld rechts außen bei der Summe 11. Die 1 und die 2 lassen sich ebenfalls einfach eintragen.

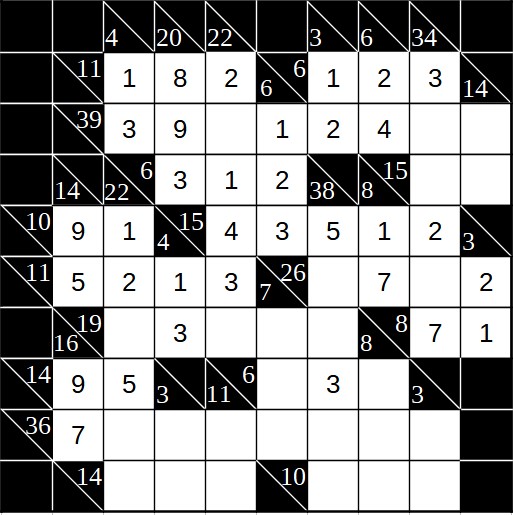
Anschließend können wir einen kleinen Trick anwenden. In der achten Zeile gibt es zweimal senkrecht die eindeutige Summe 3. Wir wissen noch nicht genau, welche Ziffer an welcher Stelle stehen muss. Aber wir können 1 und 2 jeweils als Kandidaten in die Felder eintragen:

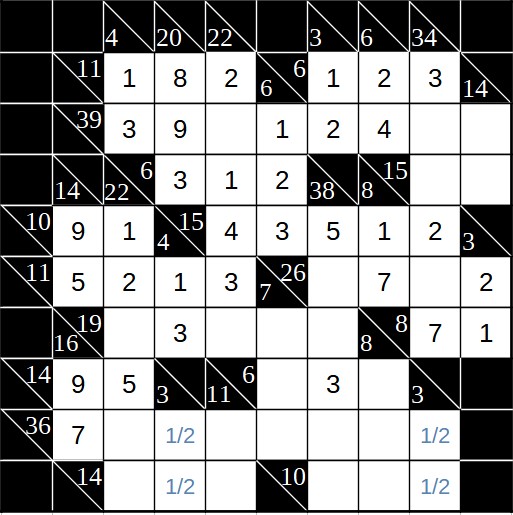
Dies hat folgenden Vorteil: In der Zeile mit Summe 36 gibt es nun zwei Felder, für die nur 1 und 2 in Frage kommen. Da in einem dieser Felder die 1 und im anderen die 2 steht, und in einer Summe keine Zahl doppelt vorkommen darf, können wir für die restlichen Felder der Summe 36 die 1 und die 2 ignorieren.

Diese Summe kreuzt sich mit der eindeutigen Summe 7 aus drei Summanden (1, 2 und 4). Die 1 und die 2 sind aber wie gesagt ja bereits vergeben, weshalb für den Schnittpunkt nur die 4 bleibt.

Zur weiteren Hilfe können wir nun für die sich kreuzenden (eindeutigen) Summen 36 und 22 die noch einzutragenden Summanden an den Rand schreiben:

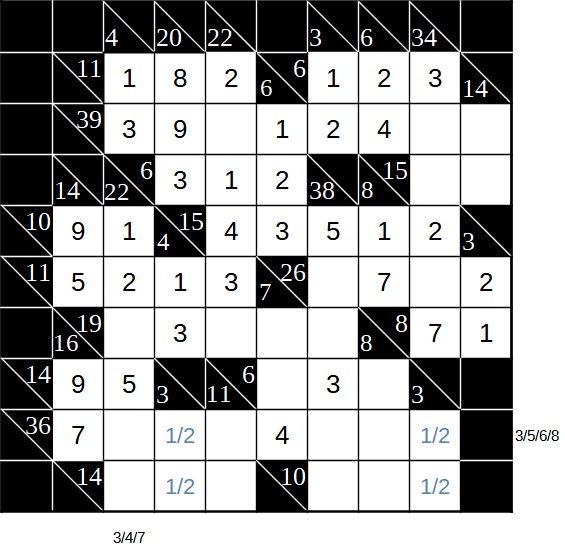
Dabei fällt auf, dass nur die 3 in beiden Summen vorkommt. Sie steht daher im Schnittpunkt. Außerdem kreuzt die 36 noch mit der Summe 8 aus drei Ziffern. Für die 36 bleiben nun nur noch die 5, die 6 und die 8 übrig. Mit dem Summanden 8 kann die Summe 8 sowieso nicht gebildet werden, aber auch mit der 6 nicht. Denn in diesem Fall hätten wir zweimal die 1 als Rest. In den Schnittpunkt von 8 und 36 muss also die 5. Damit ergibt sich diese Situation:

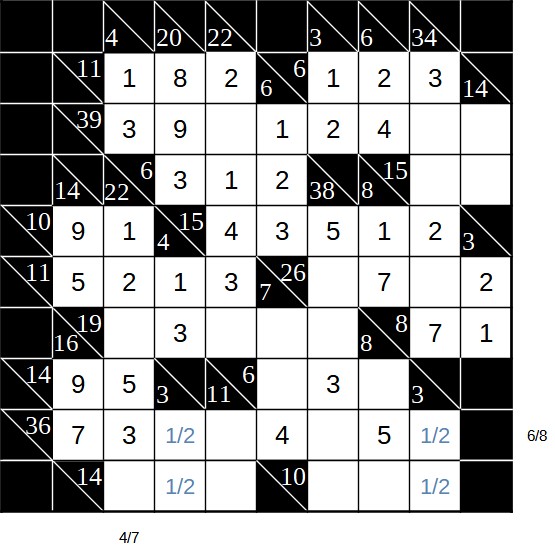
Bei der Summe 36 sind nun noch die 6 und die 8 zu vergeben. Wir können uns anschauen, welchen Einfluss diese beiden Ziffern im Schnittpunkt mit Summe 11 hätten. Wäre dort die 8, bleibe für Summe 11 für das andere Feld noch die 3. Dieses Feld ist aber auch Teil der Summe 14. In einem der Felder der Summe 14 steht entweder die 1 oder die 2. Zusammen mit der 3 würde sich also ein Rest von 9 oder 10 (nicht erlaubt) ergeben. Die 9 ist aber ebenfalls nicht möglich, da in dem freien Feld nur entweder die 4 oder die 7 stehen kann (was wir ja schon vorher an den Rand geschrieben haben). Daher können wir folgern, dass im Schnittpunkt zwischen 36 und 11 nicht die 8 stehen muss, sondern die 6. Damit lassen sich einige weitere Felder eintragen und wir bekommen folgendes Bild:

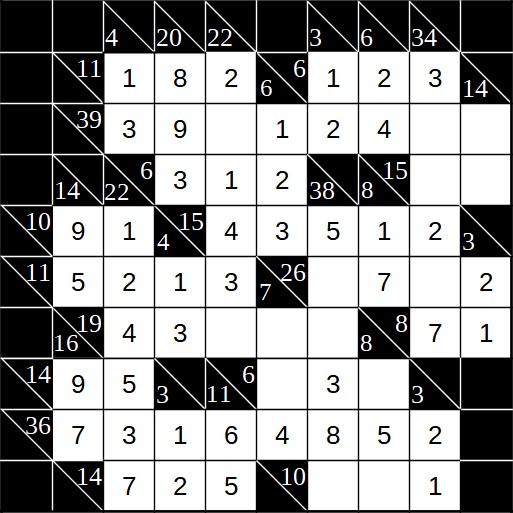
Nun sind zwar noch einige Felder auszufüllen, diese sind aber einfach. Wir können beispielsweise unten rechts bei der Summe 8 beginnen, wo die 5 bereits eingetragen ist. Bleibt ein Rest von 1 und 2. In der Zeile unten steht bereits die 1, also kommt links daneben die 2. Nun können verschiedene weitere Felder eingetragen werden und wir kommen zu folgender Situation:

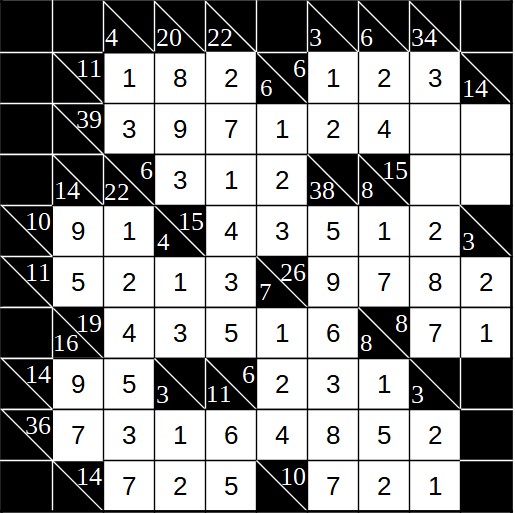
Fehlen also nur noch vier Felder. Die Summe 39 mit acht Summanden ist eindeutig. Es fehlen noch die 5 und die 8. Die 8 steht aber schon in der Summe 34. Im Schnittpunkt der beiden Summen muss also die 5 stehen. Damit haben wir die folgende Lösung: