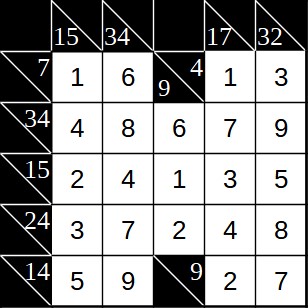
Kakuro Beispiel 1 (6x6)

Das folgende Kakuro-Beispiel gehört zu den eher einfachen Zahlenrätseln. Das heißt aber nicht unbedingt, dass jeder Schritt selbsterklärend ist und man die Zahlen wie aus der Pistole geschossen eintragen kann. Es ist durchaus einiges an Logik notwendig, um das Rätsel zu lösen. Wir gehen hier jeden Schritt einzeln durch. Es sei aber darauf hingewiesen, dass dieser Lösungsweg nur ein Vorschlag ist. Andere Wege können ebenfalls zur Lösung führen.

Es handelt sich um ein Spielfeld mit jeweils 6 Zeilen und Spalten. Das Kakuro sieht zu Beginn wie folgt aus:

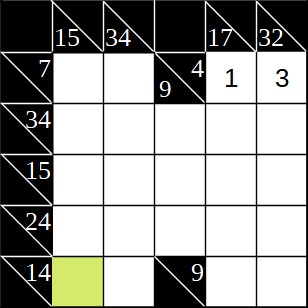
Wir können hier beispielsweise in der Ecke links oben beginnen. Dort haben wir einmal die Summe 4 (nach rechts) und die Summe 32 (nach unten). Die 4 lässt sich nur mit der Kombination 1 und 3 bilden, da alles anderen den Kakuro-Regeln widersprechen würde. Was würde nun passieren, wenn die 1 im Feld oben rechts stünde? Dann hätten wir bei der 32er-Summe eine Restsumme von 31, verteilt auf vier Felder. Das ist allerdings nicht möglich. Die höchstmögliche Summe, die sich mit vier Ziffern bilden lässt, ist 30 (=6+7+8+9). Also muss rechts oben die 3 stehen und nicht die 1.

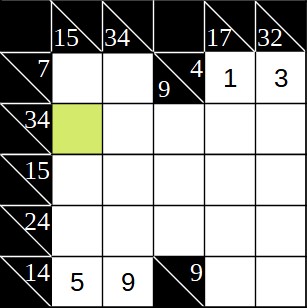
Das nächste interessante Feld ist oben grün markiert. Hier kreuzen sich die 14 mit zwei Summanden und die 15 mit fünf Summanden. Die 15 ist eine eindeutige Summe, das heißt es gibt für sie nur eine Möglichkeit: 1+2+3+4+5. Würden wir in das markierte Feld eine der Zahlen von 1 bis 4 eintragen, würde bei der 14er-Summe eine Zahl größer 9 übrig bleiben, was nicht erlaubt ist. Hier ist also nur die 5 möglich.

Auch im nächsten Schritt gehen wir ganz ähnlich heran. Hier haben wir wieder die Summe 15, für die nur noch 1, 2, 3 und 4 als Summanden übrig bleiben. Hier kreuzt die Summe 34 mit fünf Feldern. Die Logik hier ist die gleiche wie beim ersten Schritt. Würde im markierten Feld eine der Zahlen von 1 bis 3 stehen, wäre die Restsumme größer als 30. Das ist bei vier Felder aber nicht möglich, weshalb hier die 4 stehen muss.

Anschließend können wir uns wieder die Spalte ganz rechts anschauen. Da wir die 3 schon eingetragen haben, bleiben für die vier offenen Felder nur vier Kandidaten: 5, 7, 8 und 9.

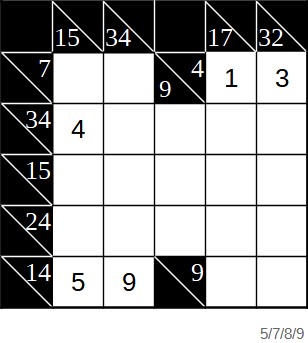
In der Mitte kreuzt sich diese Summe wieder mit einer 15 mit fünf Summanden. Hier kommen wie gesagt nur die Zahlen von 1 bis 5 in Frage. Die einzige Ziffer, die im Schnittpunkt zwischen 15 und 32 stehen kann, ist die 5 (siehe Kakuro-Strategien).

Für die Summe 32 bleiben nun nur noch 7, 8 und 9 übrig. Unten haben wir außerdem die 9 mit zwei Summanden. Hier kann die 9 nicht stehen, da ansonsten für das zweite Feld ein Rest von 0 bleiben würde. Also bleiben nur 7 und 8.

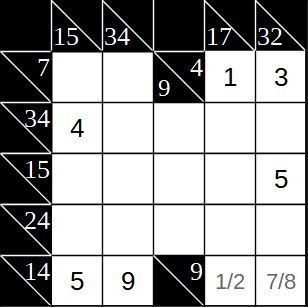
Stünde rechts unten die 8, hätten wir links daneben eine 1. Allerdings steht in der gleichen Spalte bereits eine 1 und eine Ziffer darf sich innerhalb einer Summe nicht wiederholen. Daher muss rechts unten die 7 stehen und daneben eine 2. Außerdem können wir weiter links noch eine 4 eintragen, da wir wieder die gleiche Situation haben wie vorher bereits einmal. Für die Summe 15 bleiben noch 1 bis 4 (5 steht schon in der Zeile) und die 1 bis 3 können nicht in der Summe 34 als Summanden vorkommen.

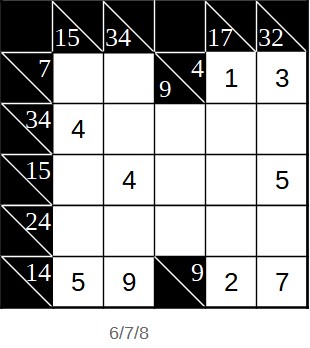
Nun können wir uns die dritte Spalte anschauen (bzw. die zweite, falls wir die schwarzen Felder links ignorieren wollen). Da die 4 und die 9 bereits eingetragen sind, gibt es für die restlichen drei Felder nur eine Möglichkeit: 6, 7 und 8. Diese Spalte kreuzt sich mit der Zeile, deren Summe 7 ist (mit zwei Summanden). Im Schnittpunkt kann nur die 6 stehen, da die 7 und 8 zu groß wären (sie würden einen Rest von 0 bzw. -1 ergeben).

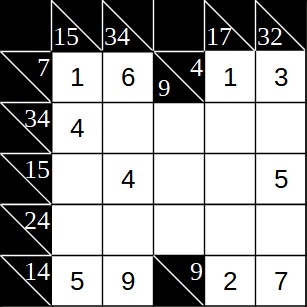
In der vierten Zeile (15) stehen bereits die 4 und die 5, also bleiben nur 1, 2 und 3. Allerdings stehen in der fünften Spalte bereist die 1 und die 2. Also bleibt für den Schnittpunkt nur die 3. Damit können wir auch ein paar weitere Felder ausfüllen, für die es nun nur noch eine Möglichkeit gibt.

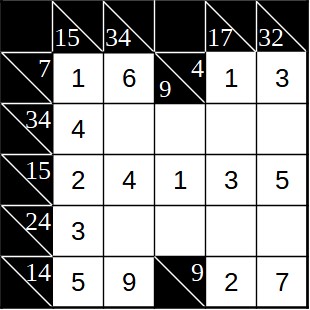
Der nächste Schritt ist von der Logik her nun etwas schwieriger. In der dritten Spalte (34) bleiben nur 7 und 8 als Optionen, in der sechsten Spalte (32) sind es 8 und 9, die noch offen sind. Wir interessieren uns jetzt dafür, welche Auswirkungen diese Felder auf die Zeile mit der Summe 24 hat.

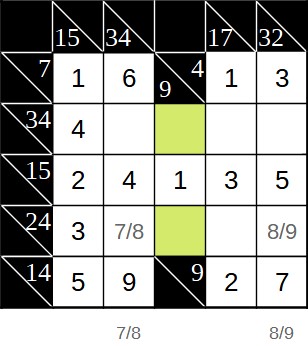
Hier ist außerdem die fünfte Spalte interessant (Summe 17). In dieser stehen bereits 1, 2 und 3. Die restlichen beiden Felder müssen also mit Zahlen von mindestens 4 belegt werden. Welche Auswirkungen hat das nun auf die Zeile mit Summe 24? Würde in dieser Zeile rechts die 9 stehen und im zweiten Feld die 8, hätten wir einen Rest von 24-9-8-3 = 4. Die im dritten Feld dieser Zeile aber wie oben beschrieben mind. eine 4 steht, ist das nicht möglich. Steht rechts aber die 9 und an der zweiten Stelle eine 7, hätten wir einen Rest von 5. Für die beiden restlichen Felder der Zeile würde also nur noch 1 und 4 in Frage kommen. Allerdings kann die 1 in keinem der Felder stehen, da sie jeweils bereits in der gleichen Spalte vorhanden ist. Daraus folgt, dass unter keinen Umständen rechts eine 9 stehen kann. Somit bleibt nur die 8 (und damit im zweiten Feld die 7). Anschließend lassen sich weitere Felder ausfüllen

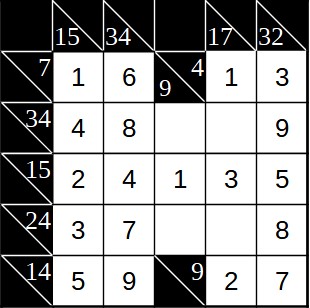
Jetzt sind wir fast fertig. Lösen kann man das Rätsel nun mit Zeile fünf (Zeilensumme 24). Hier haben wir einen Rest von 6 für die verbleibenden beiden Felder. Diese lässt sich aus 1 und 5 oder 2 und 4 bilden. 1 und 5 ist aber hier nicht möglich, die bei beiden Feldern in der Spalte schon eine 1 steht. Also bleiben 2 und 4. Die Reihenfolge ist hier auch klar, da in einer Spalte auch bereits eine 4 vorkommt.

Damit können alle Felder ausgefüllt werden. Die Lösung sieht folgendermaßen aus.